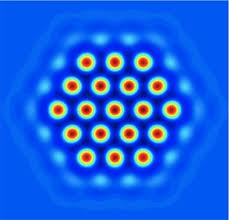
The paper “On localised hotspots of an urban crime model” by David Lloyd and Hayley O’Farrell has been accepted for publication in Physica D.  In the paper they investigate stationary, spatially localised crime hotspots on the real line and the plane of an urban crime model of Short et al (2008).  Extending the weakly nonlinear analysis of Short et al, they show in one dimension that localised hotspots should bifurcate off the background spatially homogenious state at a Turing instability provided the bifurcation is subcritical.  Using path-following techniques, they continue these hotspots and show that the bifurcating pulses can undergo the process of homoclinic snaking near the singular limit.  We analyse the singular limit to explain the existence of spike solutions and compare the analyical results with the numerical computations.  In two dimensions, we show that localised radial spots should also bifurcate off the spatially homogeneous background state.  Localised planar hexagon fronts and hexagon patches are found and depending on the proximity to the singular limit these solutions either undergo homoclinic snaking or act like “multi-spot” solutions.  Finally, we discuss applications of these localised patterns in the urban crime context and the full agent-based model.  A copy of the final form preprint can be downloaded here.