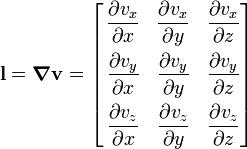The paper “Geometric invariants of the horizontal velocity gradient tensor and their dynamics in shallow water flow” has been accepted for publication in the Quarterly Journal of the Royal Meteorological Society.  The authors are Ian Roulstone, Andy White and Sid Clough.  Sid Clough is a Senior Fellow in Mathematics at Surrey, and Andy White is a Visiting Professor in Mathematics at Surrey.  An abstract of the paper follows: Divergence and vorticity are well known to be geometrically invariant quantities in that their mathematical forms are independent of the orientation of the coordinate axes.

Various other functions of the elements of the horizontal velocity gradient tensor are invariants in the same sense: examples are the resultant deformation and the determinant and Frobenius norm of the tensor. A brief account of these quadratic invariants is given, includingexpressions relating them to divergence and vorticity and to one another, and noting their occurrence in the divergence equation. Assuming shallow water dynamics with background rotation, time evolution equations for the resultant deformation and the other quadratic invariants are derived and compared. None rivals the vorticity and potential vorticity equations for compactness, but each may be written quite concisely in terms of familiar quantities. Corresponding time evolution equations under quasi-geostrophic shallow water dynamics are also derived, and lead to a simple prognostic equation for the ageostrophic vorticity.  The paper is posted on Early View at the QJ website here.