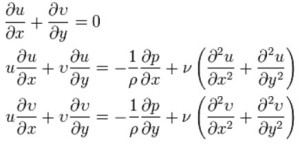The paper “Infinite-energy solutions for the Navier-Stokes equations in a strip revisited“, by Peter Anthony and Sergey Zelik, has been accepted for publication in Communications in Pure and Applied Analysis.  The paper deals with the Navier-Stokes equations in an infinite strip in the class of spatially non-decaying (infinite-energy) solutions belonging to the properly chosen uniformly local Sobolev spaces. The global well-posedness and dissipativity of the Navier-Stokes equations in a strip in such spaces has been first established in [S. Zelik, “Spatially nondecaying solutions of the 2D Navier-Stokes equation in a strip“. Glasg. Math. J., 49 (2007), no. 3, 525–588].  However, the proof given there contains a rather essential error and the aim of the present paper is to correct this error and to show that the main results of that paper remain true.  An electronic version of the accepted paper is available here.