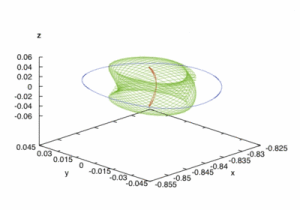
The paper “Relative Lyapunov center bifurcations“, co-authored by Claudia Wulff and Frank Schilder (Danish Technical University) has appeared online in the SIAM Journal of Applied Dynamical Systems. Relative equilibria (REs) and relative periodic orbits (RPOs) are ubiquitous in symmetric Hamiltonian systems and occur, for example, in celestial mechanics, molecular dynamics, and rigid body motion. REs are equilibria, and RPOs are periodic orbits of the symmetry reduced system. Relative Lyapunov center bifurcations are bifurcations of RPOs from REs corresponding to Lyapunov center bifurcations of the symmetry reduced dynamics. In this paper they first prove a relative Lyapunov center theorem by combining recent results on the persistence of RPOs in Hamiltonian systems with a symmetric Lyapunov center theorem of Montaldi, Roberts, and Stewart. They then develop numerical methods for the detection of relative Lyapunov center bifurcations along branches of RPOs and for their computation. They apply the methods to Lagrangian REs of the N-body problem.  The paper is announced on the SIADS website here.