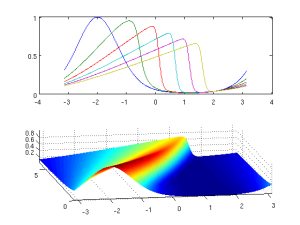
The paper “Degenerate hyperbolic conservation laws with dissipation: reduction to and validity of a class of Burgers-type equations“, co-authored by Tom Bridges, Jon Pennant, and Sergey Zelik, has been accepted for publication in the the journal Archives for Rational Mechanics and Analysis.  A hyperbolic conservation law is said to be degenerate or critical if the Jacobian of the flux vector evaluated on a constant state has a zero eigenvalue.  In the paper, it is proved that a degenerate conservation law with dissipation will generate dynamics on a long time scale that resembles Burger’s dynamics. The case of k-fold degeneracy is also treated, and it is shown that it leads to a reduction to a quadratically coupled k-fold system of Burgers-type equations. A novelty is that validity of the reduction and existence in the reduced system is proved in the class of uniformly local spaces, thereby capturing both finite and infinite energy solutions. The theory is applied to some examples, from stratified shallow-water hydrodynamics, that model the birth of hydraulic jumps.  The final form preprint can be downloaded here.