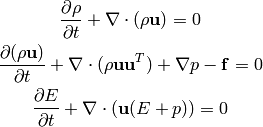Bin Cheng‘s paper “Improved accuracy of incompressible approximation of compressible Euler equations” has been accepted for publication in the SIAM J Mathematical Analysis.  The article addesses a fundamental concern regarding the incompressible approximation of fluid motions, one of the most widely used approximations in fluid mechanics.  Common belief is that its accuracy is of the order of the Mach number to the first power.  In the paper, Bin proves an order Mach number squared accuracy for the incompressible approximation of the isentropic, compressible Euler equation, thanks to several decoupling properties. At the initial time, the velocity field and its derivatives should be of order unity, but the boundary conditions can be as stringent as the solid-wall type.  The fast acoustic waves are still of the order of the Mach number, since the error is measured in the sense of Leray projection and more physically, in time averages.  The paper also shows that when a passive scalar is transported by the flow, it is of order Mach number squared, pointwise in time, to use the incompressible velocity field in the transport equation.  A final form preprint can be downloaded here.