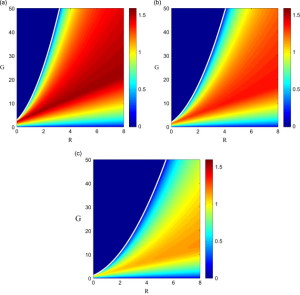
The paper “Instability of sloshing motion in a vessel undergoing pivoted oscillations“, co-authored by Matt Turner, Hamid Alemi Ardakani, and Tom Bridges, has been accepted for publication in the Journal of Fluids and Structures.  The in press version can be found on the JFS website.  The paper studies the instability of a suspended rectangular vessel partially filled with an inviscid fluid.  This configuration produces an interesting physical model for investigating the dynamic coupling between the fluid and vessel motion. The fully nonlinear, two-dimensional, equations of motion are derived and linearised for small-amplitude vessel and free-surface motions, and the natural frequencies of the system analysed. It is found that the linear problem exhibits an unstable solution if the rod length is shorter than a critical length which depends on the length of the vessel, the fluid height and the ratio of the fluid and vessel masses. In addition, we identify the existence of 1:1 resonances in the system where the symmetric sloshing modes oscillate with the same frequency as the coupled fluid/vessel motion. The implications of instability and resonance on the nonlinear problem are also briefly discussed.