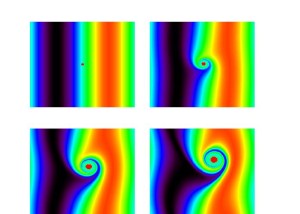
Matt Turner‘s paper “Temporal evolution of vorticity staircases in randomly strained two-dimensional vortices” has been accepted for publication in Physics of Fluids.  In the paper, the evolution of a Gaussian vortex subject to a weak-external-random n-fold multipolar strain field is examined using fully nonlinear simulations. The simulations show that at large Reynolds numbers, fine scale steps form at the periphery of the vortex, before merging, generally leaving one large step, which acts as a barrier between the vorticity within the coherent core and the surrounding, well mixed, “surf zone.”  The published version of the paper is available here.