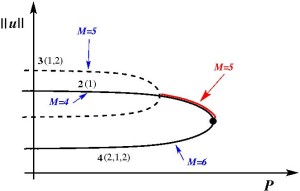
The paper “Transversality of homoclinic orbits, the Maslov index, and the symplectic Evans function” co-authored by Frédéric Chardard (Université Jean Monnet) and Tom Bridges has been accepted for publication in Nonlinearity.  Homoclinic orbits of Hamiltonian systems have two important geometric invariants: a Maslov index and a Lazutkin–Treschev invariant. A new relation between the two has been discovered and is moreover linked to transversal construction of homoclinic orbits: the sign of the Lazutkin–Treschev invariant determines the parity of the Maslov index. A key tool is the geometry of Lagrangian planes. All this geometry feeds into the linearization about the homoclinic orbit in the time-dependent system, which is studied using the Evans function. A new formula for the symplectification of the Evans function is presented, and it is proven that the derivative of the Evans function is proportional to the Lazutkin–Treschev invariant.  Examples from the theory of gradient reaction–diffusion equations and pattern formation are presented. The webpage for the published paper is here.