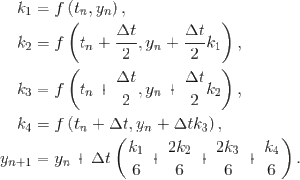Claudia Wulff‘s paper, co-authored with Marcel Oliver (Jacobs University, Germany), on “Exponentially accurate Hamiltonian embeddings of symplectic A-stable Runge-Kutta methods for Hamiltonian semilinear evolution equations“, has been accepted for publication in the Proceedings of the Royal Society of Edinburgh.  A final-form pre-print can be found here.  In this paper it is proved that a class of A-stable symplectic Runge-Kutta semidiscretizations — applied to a class of semilinear Hamiltonian PDEs which are well-posed on spaces of analytic functions with analytic initial data — can be embedded into a Hamiltonian flow up to an exponentially small error. This paper is the third in a series of papers on the subject.  The first two can be found here and here.