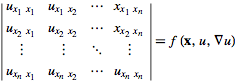The paper “Monge–Ampère structures and the geometry of incompressible flows” co-authored by B Banos (Université de Bretagne Sud, France), V. Roubtsov (Université d’Angers, France), and Ian Roulstone, has just been published online by Journal of Physics A: Mathematical and Theoretical. A link to the journal page is here.  The paper shows how a symmetry reduction of the equations for incompressible hydrodynamics in three-dimensions leads naturally to Monge–Ampère (MA) structure, and Burgers’-type vortices are a canonical class of solutions associated with this structure. The mapping of such solutions, which are characterised by a linear dependence of the third component of the velocity on the coordinate defining the axis of rotation, to solutions of the incompressible equations in two-dimensions is also shown to be an example of a symmetry reduction. The MA structure for incompressible flow in two-dimensions is shown to be hyper-symplectic.