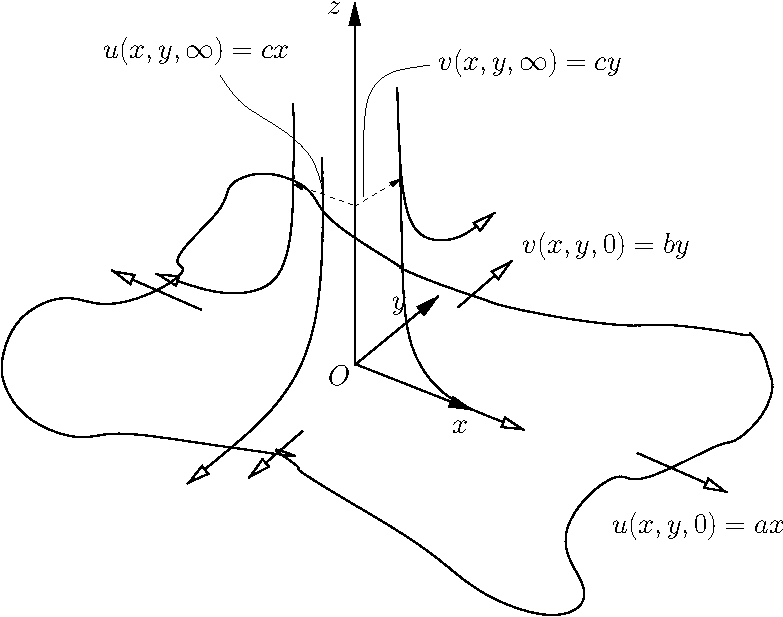
The paper “Homann stagnation-point flow impinging on a biaxially stretching surface“, coauthored by Matt Turner and Patrick Weidman (University of Colorado), has been accepted for publication in the European Journal of Mechanics B/Fluids. The paper identifies exact solutions to the Navier-Stokes equations when a stretching surface is placed below a stagnation point flow. Four branches of solutions are found in the surface shear stress parameter space, and for sufficiently small stretches these exhibit a multi-branch spiralling behaviour. The author final copy of the paper can be found here. A figure from the paper showing a schematic of the flow is below.