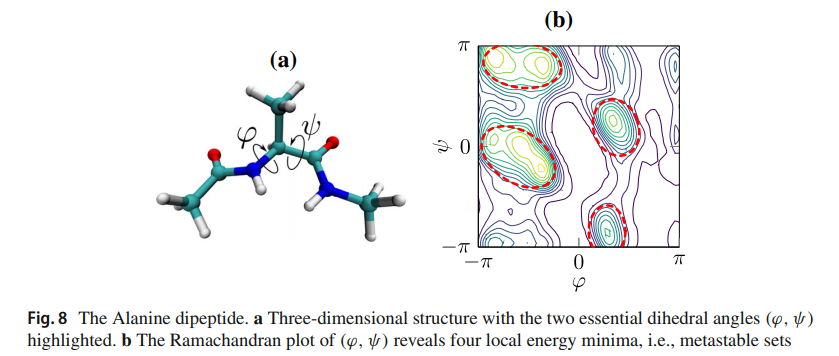
The paper “Dimensionality reduction of complex metastable systems via kernel embeddings of transition manifolds“, co-authored by Andreas Bittracher (FU Berlin), Stefan Klus, Boumediene Hamzi (Imperial & AlFaisal), Péter Koltai (FU Berlin) & Christof Schütte (Zuse Institute), has been published in the Journal of Nonlinear Science. The paper presents a novel kernel-based machine learning algorithm for identifying the low-dimensional geometry of the effective dynamics of high-dimensional multiscale stochastic systems. The published version is open access and available here. The screenshot below shows Figure 8 from the paper.