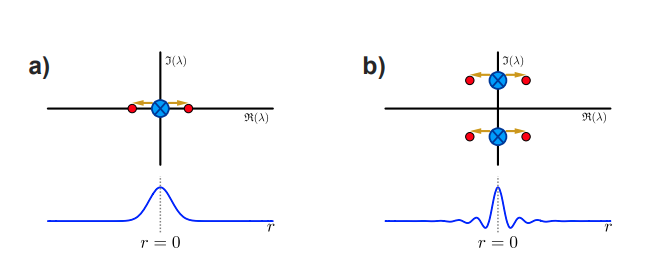
The paper “Existence of localised radial patterns in a model for dryland vegetation“, with sole author Dan Hill, has been published in the IMA Journal of Applied Mathematics. The published version is here and the arXiv version is here. The paper considers stationary localised radial solutions to a reduced model for dryland vegetation on flat terrain. By considering certain prototypical pattern-forming systems, the paper proves the existence of three classes of localised radial patterns bifurcating from a Turing instability. Additionally, numerical solutions are presented, based on continuation methods, to study the bifurcation structure and radial stability of localised radial spots and gaps. The image below shows Figure 2 from the paper.