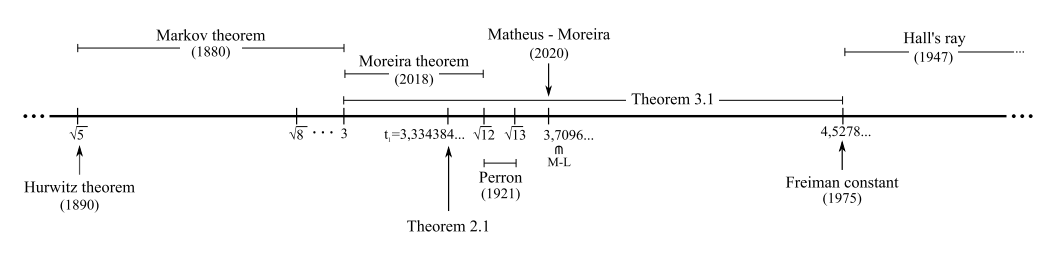
The paper “Hausdorff dimension of Gauss–Cantor sets and two applications to classical Lagrange and Markov spectra“, co-authored by Carlos Matheus (École Polytechnique), Carlos Gustavo Moreira (Nankai University, China & IMPA, Brazil), Mark Pollicott (Warwick), and Polina Vytnova, has been published in the November issue of Advances in Mathematics (link to the published version here). The paper is dedicated to the study of two important subsets of the real line, namely Lagrange spectrum and Markov spectrum. The first main result (Theorem 2.1) provides a rigorous estimate on the smallest value t1 such that the portion of the Markov spectrum (−∞,t1)∩M has Hausdorff dimension 1. The second main result (Theorem 3.1) gives a new upper bound on the Hausdorff dimension of the set difference M∖L. In addition, the paper presents a plot of the dimension function, which hasn’t appeared previously in the literature. The image below (Figure 2 from the paper) shows how Theorems 2.1 and 3.1 fit into the history of the subject. (Click on the image for a larger version.)