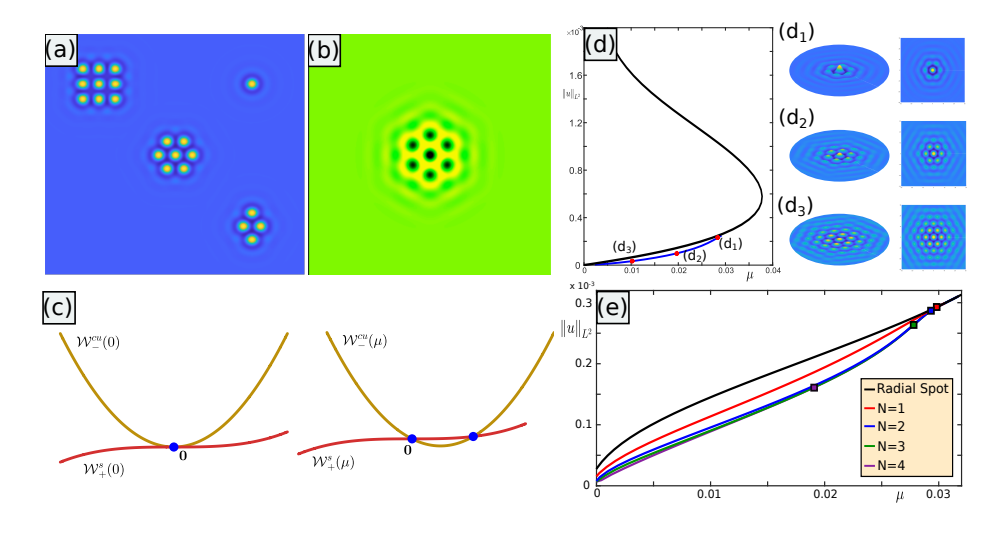
The 60-page paper “Approximate localised dihedral patterns near a Turing instability“, co-authored by Dan Hill (Saarlandes, Germany), Jason Bramburger (Concordia, Canada), and David Lloyd, has been accepted for publication in Nonlinearity. The final form preprint can be found on the arXiV (link here). The paper presents a comprehensive approach to the problem of localised 2D patterns by using techniques developed in the study of axisymmetric patterns. The analysis covers localised patterns equipped with a wide range of dihedral symmetries, avoiding a restriction to solutions on a predetermined lattice. The image below is a screenshot of Figure 1 of the paper.