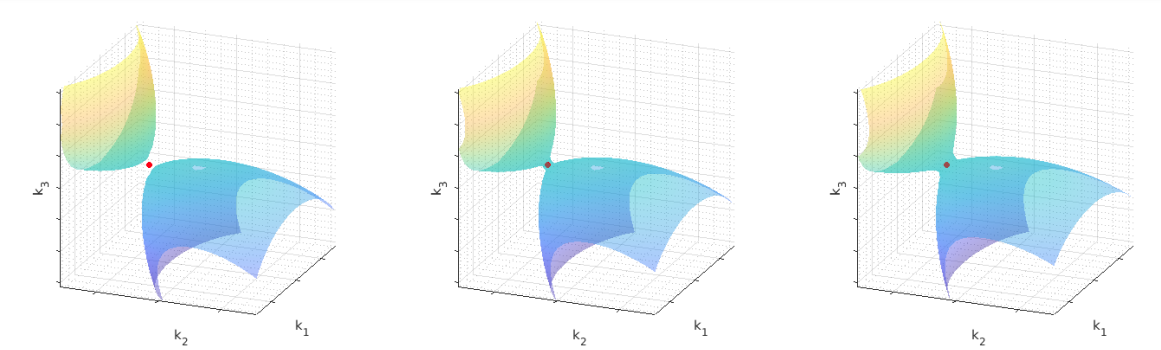
The 55-page paper “Near-resonance approximation of rotating Navier-Stokes equations“, co-authored by Bin Cheng and Zisis Sakellaris, has been published open access in the journal Nonlinearity (link to IOP website here). In the paper they formalise the concept of “near resonance” for the rotating Navier-Stokes equations, and prove that the family of proposed PDEs is globally well-posed for any rotation rate and inital datum of any size in H^s, with s>0. Full abstract and details can be found at the above link. The image below shows the topological change of the level sets on the boundary of the near resonant set in wavenumber space. Below the image is a screenshot of the first main theorem of the paper.