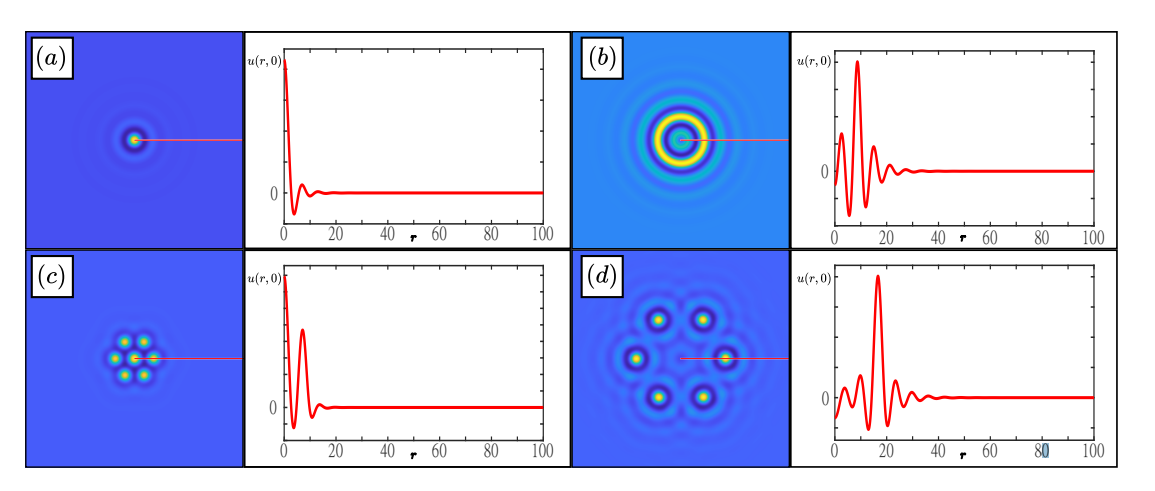
The paper “Dihedral rings of patterns emerging from a Turing bifurcation“, co-authored by Dan Hill (Universität des Saarlandes), Jason Bramburger (Concordia University), and David Lloyd, has been accepted for publication in Nonlinearity. A final form preprint is on the arXiv (link here). The paper proves that approximate strongly interacting patterns can emerge in various ring-like dihedral configurations, bifurcating from quiescence near a Turing instability in generic two-component reaction-diffusion systems. The analysis is complemented by numerical investigations. The screenshot below shows Figure 1 from the paper.