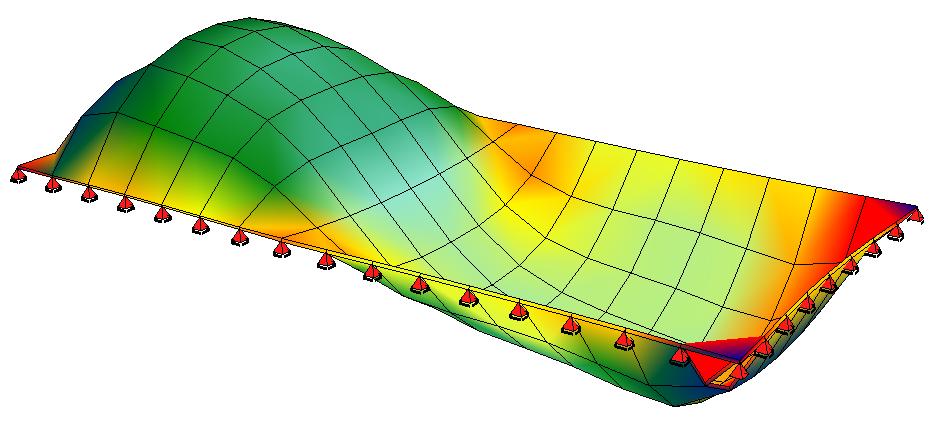
The paper “A continuously perturbed Dirichlet energy with area-preserving stationary points that ‘buckle’ and occur in equal-energy pairs“, co-authored by Jon Bevan and Jonathan Deane, has been accepted for publication in Nonlinear Differential Equations and Applications (a link to the journal webpage is here). The paper exhibits a family of parameter-dependent convex functionals with infinitely many, equal-energy differentiable stationary points. A bifurcation (buckling point) is found at a critical value of the parameters, with interesting properties. They also find Lagrange multipliers associated with the maps and estimate their asymptotics.The paper proves a range of other rigorous results about these maps.