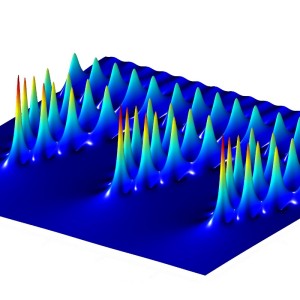
Tom Bridges gave at talk in the Dynamical Systems Seminar at Imperial College on Thursday 28 February.  The title of the talk is “How modulation generates geometry in dynamical systems and nonlinear waves“.  An abstract of the talk follows.  The backbone of the talk is “modulation”; specifically what to modulate and how modulation generates geometry.  The talk is based on three examples.  (1D modulation) how modulation gives a new viewpoint on elementary homoclinic bifurcation with curvature of modulation determining the coefficient of the nonlinear term.  (2D modulation) the mythical origins of the KdV equation are given a new perspective, resulting in a universal form for emergence and how geometry of modulation determines the coefficients, and a dynamical systems argument determines the dispersion. Considering that the classical derivation of KdV is about the trivial solution, a by-product of the result is how to modulate the trivial solution!  (3D modulation) The third example will show how modulation of periodic solutions leads to a sequence of multi-pulse planforms in PDEs like the Swift-Hohenberg equation.  This theory is deduced by deriving a new modulation equation in two space dimensions and time.