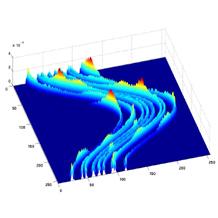
 The paper “Computing the invariant measure and the Lyapunov exponent for one-dimensional maps using a measure-preserving polynomial basis“, by Philip Aston and Oliver Junge (TU Munich) has been accepted for publication in the journal Mathematics of Computation. The paper considers a generalization of Ulam’s method for approximating invariant densities of one-dimensional chaotic maps. Rather than use piecewise constant polynomials to approximate the density, polynomials of degree n are used which are defined by the requirement that they preserve the measure on n+1 neighboring subintervals. Over the whole interval, this results in a discontinuous piecewise polynomial approximation to the density. Error results are proved where this approach is used to approximate smooth densities. Also considered are the computation of the Lyapunov exponent using the polynomial density and it is shown that the order of convergence is one order better than for the density itself. Together with using cubic polynomials in the density approximation, this yields a very efficient method for computing highly accurate estimates of the Lyapunov exponent. The theoretical findings are illustrated with some examples.
The paper “Computing the invariant measure and the Lyapunov exponent for one-dimensional maps using a measure-preserving polynomial basis“, by Philip Aston and Oliver Junge (TU Munich) has been accepted for publication in the journal Mathematics of Computation. The paper considers a generalization of Ulam’s method for approximating invariant densities of one-dimensional chaotic maps. Rather than use piecewise constant polynomials to approximate the density, polynomials of degree n are used which are defined by the requirement that they preserve the measure on n+1 neighboring subintervals. Over the whole interval, this results in a discontinuous piecewise polynomial approximation to the density. Error results are proved where this approach is used to approximate smooth densities. Also considered are the computation of the Lyapunov exponent using the polynomial density and it is shown that the order of convergence is one order better than for the density itself. Together with using cubic polynomials in the density approximation, this yields a very efficient method for computing highly accurate estimates of the Lyapunov exponent. The theoretical findings are illustrated with some examples.
