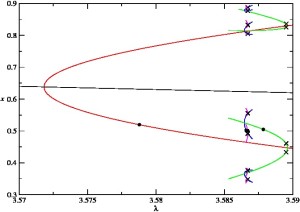
The paper of Philip Aston and Neil Bristow on “Alternating period doubling cascades” has been accepted for publication in Nonlinearity.  In the paper, they consider period-doubling cascades in two-dimensional iterated maps in which forward and backward period-doubling bifurcations alternate to form an alternating period-doubling cascade. By tracking the eigenvalues of a typical map through such a cascade they show that two-dimensional maps may give rise to two qualitatively different alternating period-doubling cascades.  They apply renormalisation theory to one class of alternating period-doubling cascades, and derive universal spatial scalings for such cascades from fixed points of the appropriate renormalisation operator.  They also derive universal parameter scalings for these cascades from the eigenvalues of the linearisation of the renormalisation operator. The theory is illustrated by an example.