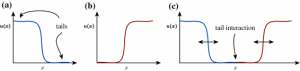
The paper “Computing interacting multi-fronts in one-dimensional real Ginzburg Landau equations“, co-authored by Tasos Rossides, David Lloyd and Sergey Zelik, has been accepted and published in the Journal of Scientific Computing.   In the paper they develop an efficient and robust numerical scheme to compute multi-fronts in one-dimensional real Ginzburg–Landau equations that range from well-separated to strongly interacting and colliding. The scheme is based on the global centre-manifold reduction where one considers an initial sum of fronts plus a remainder function (not necessarily small) and applying a suitable projection based on the neutral eigenmodes of each front. Such a scheme efficiently captures the weakly interacting tails of the fronts. Furthermore, as the fronts become strongly interacting, they show how they may be added to the remainder function to accurately compute through collisions.  They also discuss how this numerical scheme can be extended to general PDE systems and other multi-localised structures.  The published paper can be downloaded here.