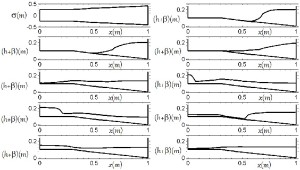
The paper “Shallow-water sloshing in a moving vessel with variable cross-section and wetting-drying using an extension of George’s well-balanced finite volume solver” with authors Hamid Alemi Ardakani, Tom Bridges and Matt Turner has been accepted for publication in the Journal of Computational Physics.  The shallow-water equations in a moving vessel with variable bottom topography and variable cross-section with wetting and drying are considered. A class of Roe-type upwind solvers for the system of balance laws is derived which respects the steady-state solutions. The theory is then extended to solve the shallow-water flows in moving vessels with arbitrary cross-section with influx-efflux boundary conditions motivated by the shallow-water sloshing in the OWEL ocean wave energy converter.  The numerical solutions are compared to an extended new Roe-type solver for the system of balance laws with a time-dependent source function. The shallow-water sloshing finite volume solver is coupled to a Runge-Kutta integrator for the vessel motion.