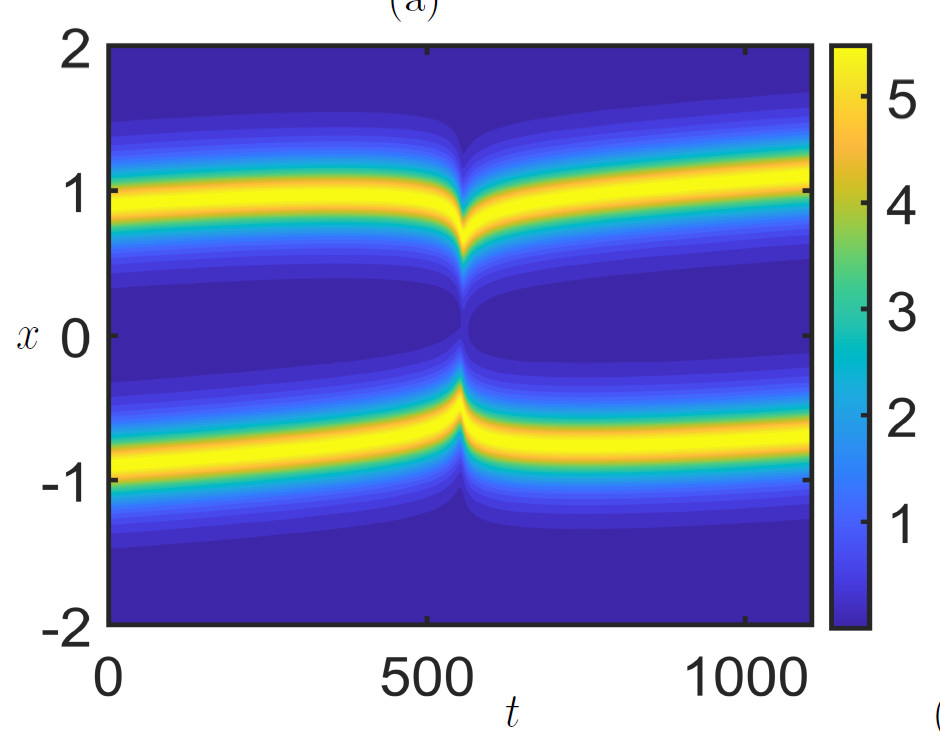
The paper “The dynamics of interacting multi-pulses in the one-dimensional quintic complex Ginzburg-Landau equation” co-authored by Tasos Rossides (PhD student of Lloyd & Zelik), David Lloyd, Sergey Zelik and Matt Turner has been accepted for publication in the SIAM Journal on Applied Dynamical Systems. The paper presents a novel numerical approach which allows for the accurate numerical calculation of  multi-pulse interaction in the complex Ginzburg-Landau equation. The efficient scheme uses a global centre-manifold reduction by considering the solution to be the sum of the individual pulses plus a remainder term. The centre-manifold reduction reduces the scheme to a set of slow ODEs for the position and phase of the pulses, and a fast PDE for the remainder function. Asymptotics are then used to write the fast-slow system as a set of second order equations  in terms of the pulse separation distance to speed up their solution. Results are presented for two- and three-pulse interactions. For the two-pulse problem in particular, the phase plane consists of cells of periodic behaviour, separated by an infinite set of heteroclinic orbits. This numerical scheme can show that these heteroclinic orbits ‘split’ under the perturbation creating complex spiral behaviour. The author final copy of the paper can be found here or on the arxiv.The image below shows a two-pulse solution from Figure 5 in the paper.