A new paper has appeared today in the journal Quantum Machine Intelligence written by our PhD student Joe Gibbs (along with an internal PhD supervisor and external collaborator). The paper describes his work on developing algorithms for current and future quantum computers to simulate real physical systems.

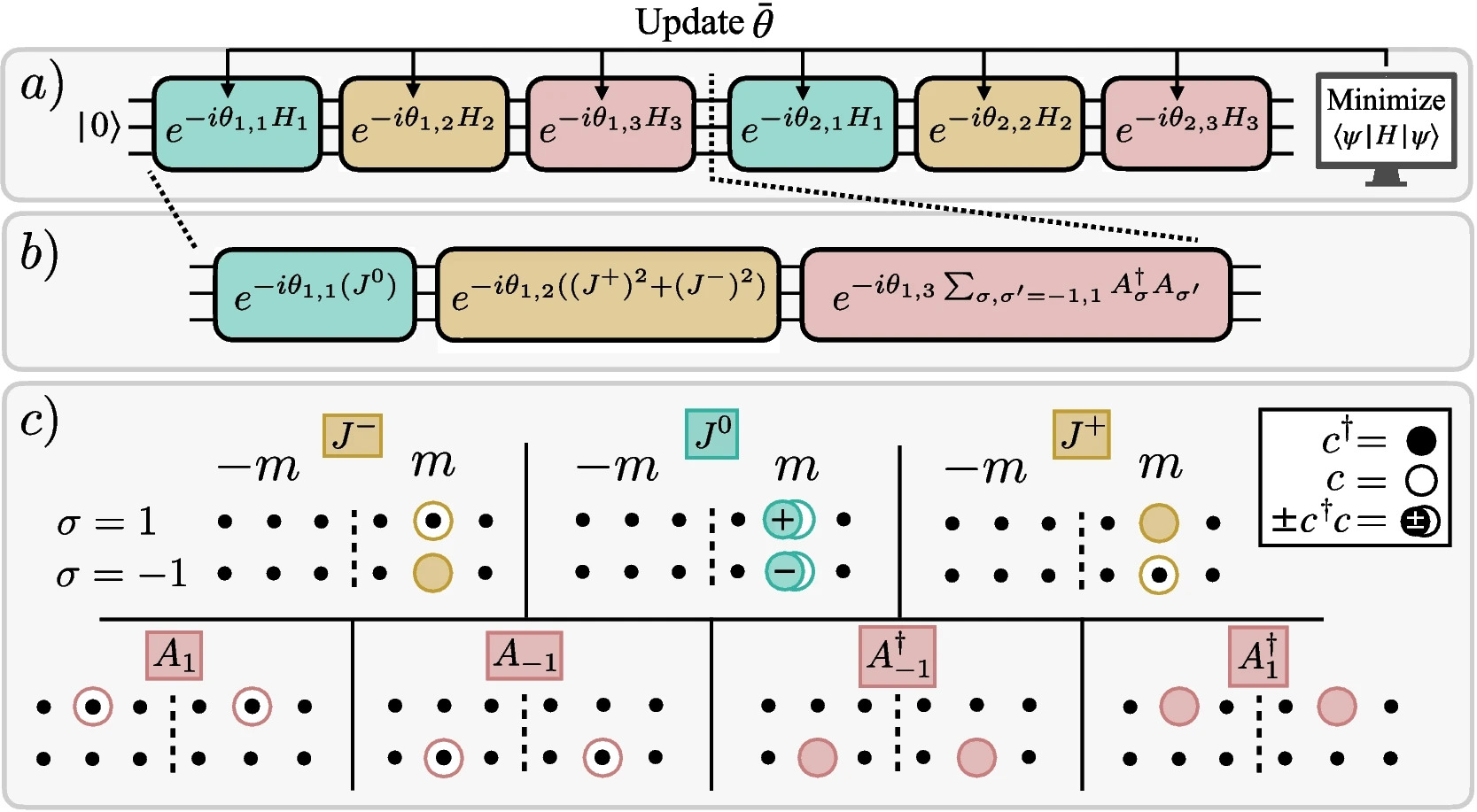
He took a simple model of the nucleus in which the most weakly-bound nucleons are free to move in two neighbouring energy levels, and made the first application of a particular kind of quantum computing technique – the Hamiltonian Variational Ansatz – to attempt to match up the state of the quantum computer to that of the nuclear system as closely as possible.

One of the main uses of quantum computers within the physical sciences is in quantum simulation, where a physical problem on interest (e.g. the structure of a nucleus in our case) is mapped on to the individual elements, called qubits, of a quantum computer. Joe’s work shows that we can make use of known symmetries of the nuclear system to make much better starting guesses of the nuclear states we want to simulate on the quantum computer compared to standard methods. This state preparation problem is equivalent to solving the Schrödinger equation – the basic equation of quantum mechanics, and is no mean feat. The aim of the wider project is to make use of the fantastic scaling properties of a quantum computer to simulate nuclear systems which are too unwieldy and complicated to be simulated on a classical computer.

The paper is open access, and you can see it here. The first picture which shows a kind of schematic of the problem and the algorithm is below: